Infotaxis
This project demonstrates the infotaxis algorithm based on Bayes’ update to guide a robot’s navigation of a finite space to find the source of a signal.
Video Demo
The Algorithm
The infotaxis algorithm uses Bayes’ update to make informed decisions about what the belief regarding the environment will be if certain motions and sensor readings in the environment are made. In this case, the idea is to maximize information gain with each move the robot makes such that the robot makes the optimal move to search for the source of a signal.
The math for this project can be found on page 50 of these notes on activce learning: Notes
Robot Sensor Setup
In the inital Bayes’ Update investigation, the sensor on the robot was assumed to be a binary reading right at the location of the measurement. Since most sensors in robotics can sense over a range of space, the sensor here is assumed to have a gradient of fidelity based on a binary reading. The plot below shows the shape of the sensor’s field as well as the strength of the sensor’s read.
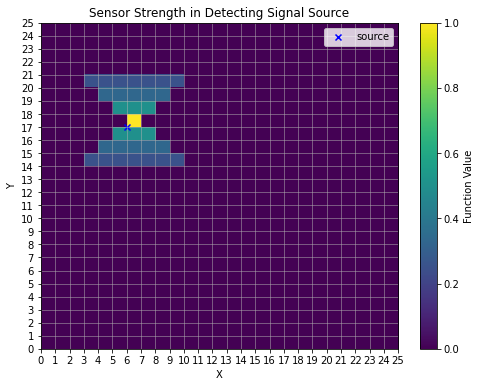
In this plot, the finite space is defined by a 25x25 cell grid which could be thought of like an occupancy grid. The sensor field is shown to resemble a dumbbell shape where if the robot’s sensor is directly over the source of the signal, then the sensor will have a probability of 1.0 reading the signal. As the field of the sensor extends up and down, the fidelity drops to 0.5, 0.333, and 0.25 before it eventually has no range. The sensor also had no range to the sides in this fashion.
It is important to note that this is still a binary signal, so while the robot knows the result of the measurement, it does not know WHERE in the sensor field the signal triggered. What this means is that the robot can make inferences about it’s surrounding area based on signal strength rather than just in the exact location of the robot. This for instance means that if the signal reads negative, the robot will know with 100% certainty that it is NOT directly on top of the source, it is 50% sure the source is not directly above or below, and so on.
Finding the Source via a Random Walk
In the below plots, we see the grid cells colored to represent the belief that each cell is the source. This is a probability that when summed over the entire space will equal 1.0, and the lighter the color, the greater the belief that the location could be the signal source.
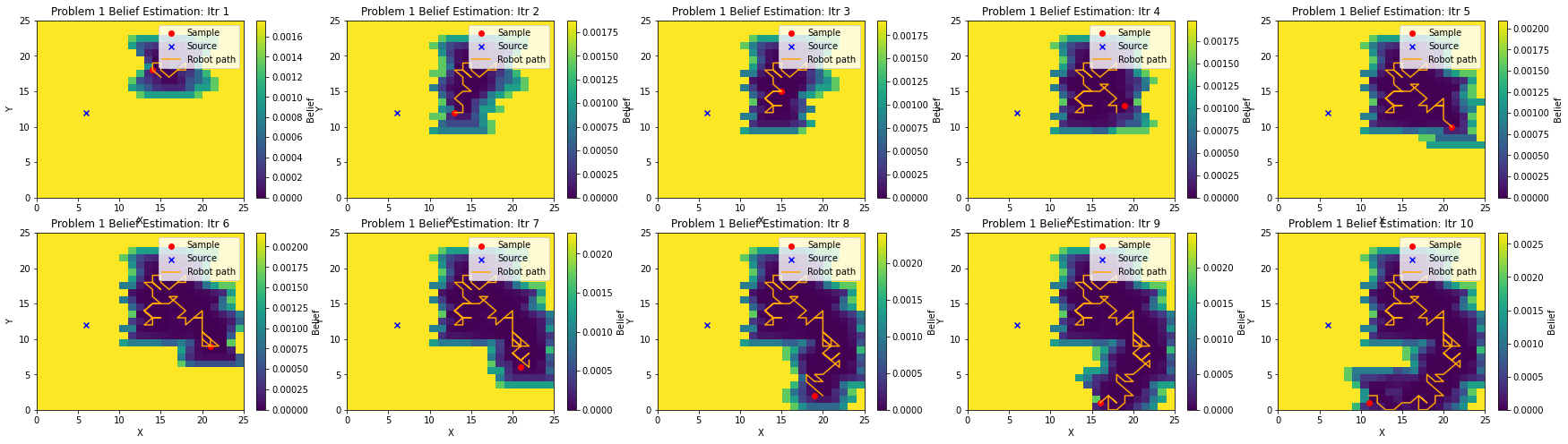
In this implementation, the robot moves around the grid via a simple random walk algorithm taking a sample at each location. Each iteration of the plot shows the path of the robot and the current belief over the space after 10 moves. While the plots show that the robot learned more about the environment by moving, it is clear that a random walk algorithm is not the most efficient, and after 100 moves, it could not pinpoint the source of the signal (the blue “x”).
In the above iteration of this experiment, the random walk was able to narrow the belief down considerably to just a few spots thanks to a few positive reads, but unfortunately, the source was incorrectly identified. As the robot explores, a positive read can eliminate all cells outside of the “dumbbell” FOV of the sensor as being the source, but because it cannot identify where in the FOV the sensor was triggered, the robot did not narrow the belief correctly over the source even though it is reporting nearly 50% confidence as shown by the upper end of the color bar.
Navigating Using Infotaxis
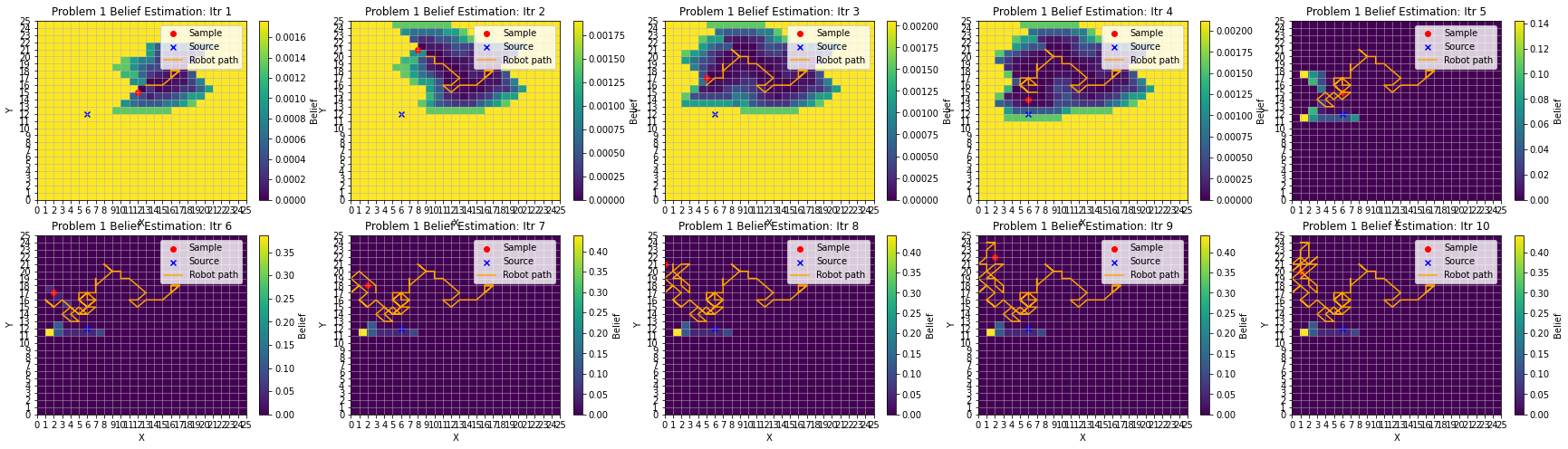
If the robot is now given the choice of moving towards the direction that is most “interesting” (maximizing information gain), the robot can move in a much more efficient manner. In this example, the robot have 5 choices: up, down, left, right, or stay. Using the infotaxis algorithm, the robot makes the choice to move, takes a measurement, and updates the belief matrix to then run through this cycle again.
Like the random walk, this robot is still given 100 moves to make (plotted in groups of 10), though unlike the random walk, the robot moves in a much more methodical fashion. Eventually the robot is able to locate the source of the signal with near perfect certainty.
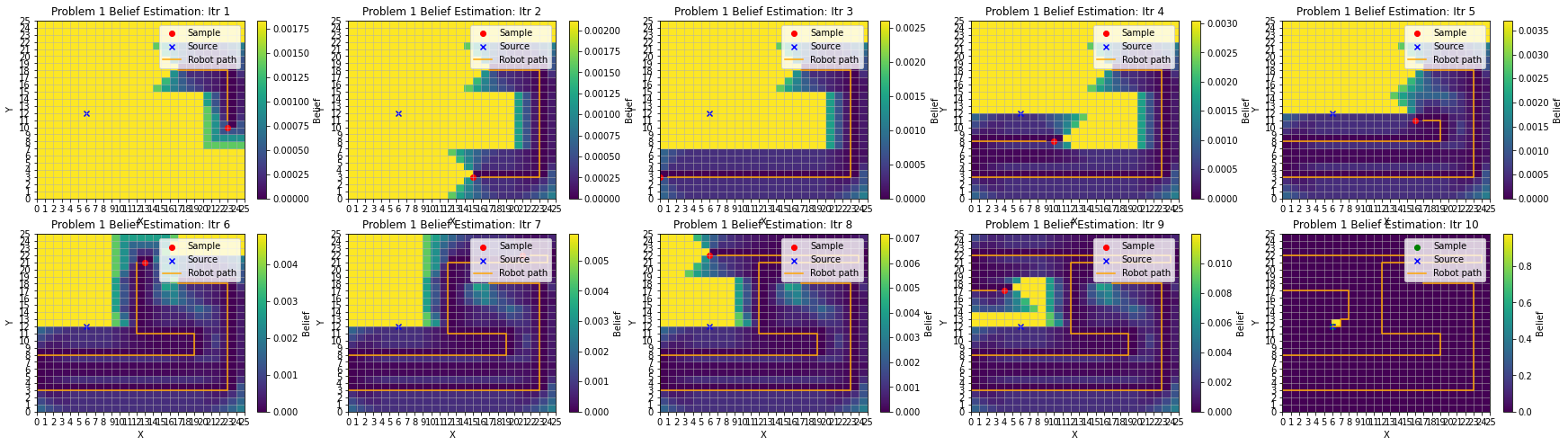
If we run this experiment again with the infotaxis algorithm starting from a different initial location, we see the robot is able to again find the source, but it also displays some other interesting behavior.
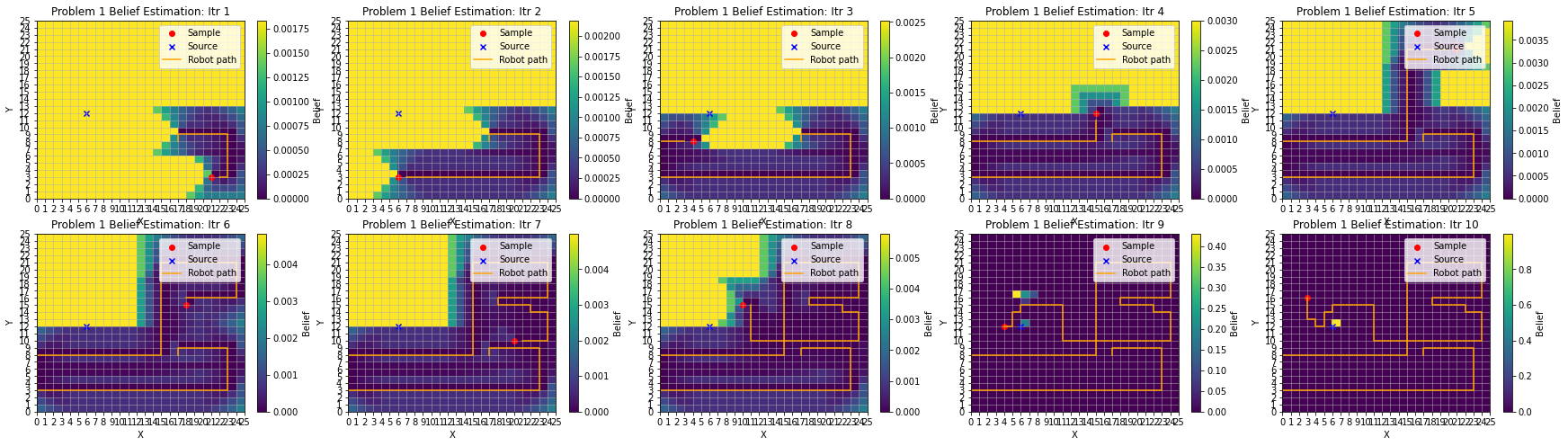
As seen above, the robot moved methodically often seeking out the brightest nearby space to investigate, and it also succeeds in finding the source with high confidence. Unlike the first infotaxis run but similar to the random walk experiments, the robot, as seen in Itr 9, finds itself with a couple potential options for where the source is, and it also finds itself initially guessing a high confidence on a cell that is NOT the source. Because the robot has the ability to move in a way that maximizes information gain using infotaxis, it is able to correct this and still zero in on the source location.
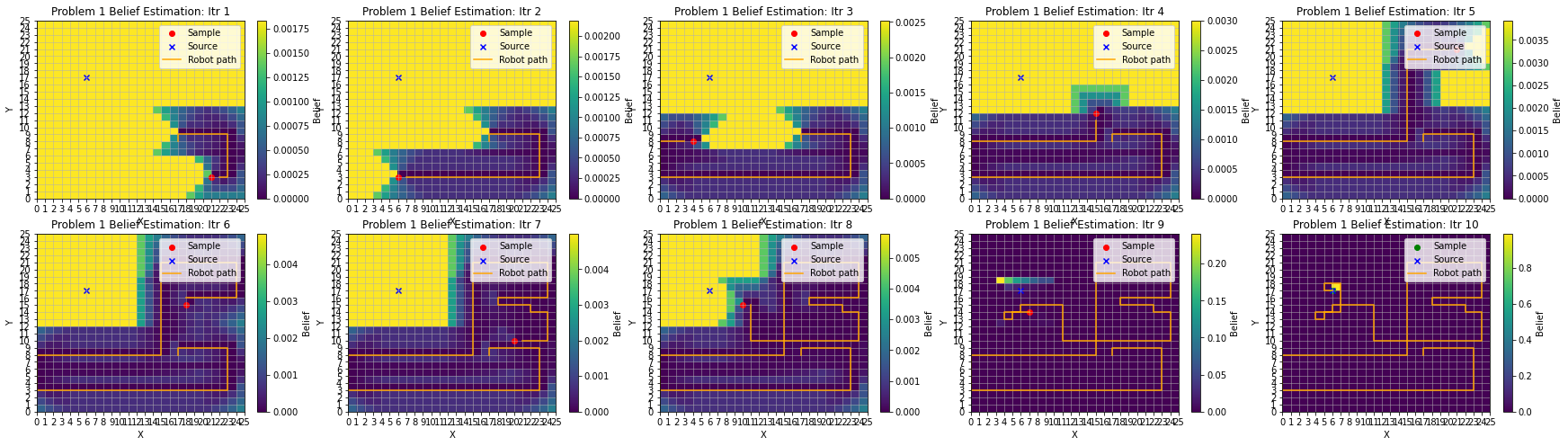
If the experiment is run a third time with a new starting location and source location, we see a similar behavior and result as the second run.
Closing Thoughts
Overall this exploration demonstrates that infotaxis can be an efficient driver for autonomous mapping for robots. One consideration is the simplicity of this example versus real life applications. This robot has a finite space to explore with a single binary sensor with which to calculate the change in entropy. This means that there are only 10 possibilities per move (positive or negative result for each possible move on the grid). In real life applications, sensors produce data over a more continuous rather than discrete set of results which means that the scaling for the update becomes significantly more computationally heavy.
I am interested to investigate algorthms involving mutual information like Fast Shannon Mutual Information (FSMI) to help solve this problem and scale real sensor data more appropriately.
Code
This code can be downloaded as an ipynb or run via google colab and run for yourself.
