2D Die in a Cup Simulation from Scratch
This project simulates a die colliding in a spinning cup by modeling the Lagrangian dynamics in this 6 DoF system.
Video Demo
Project Setup
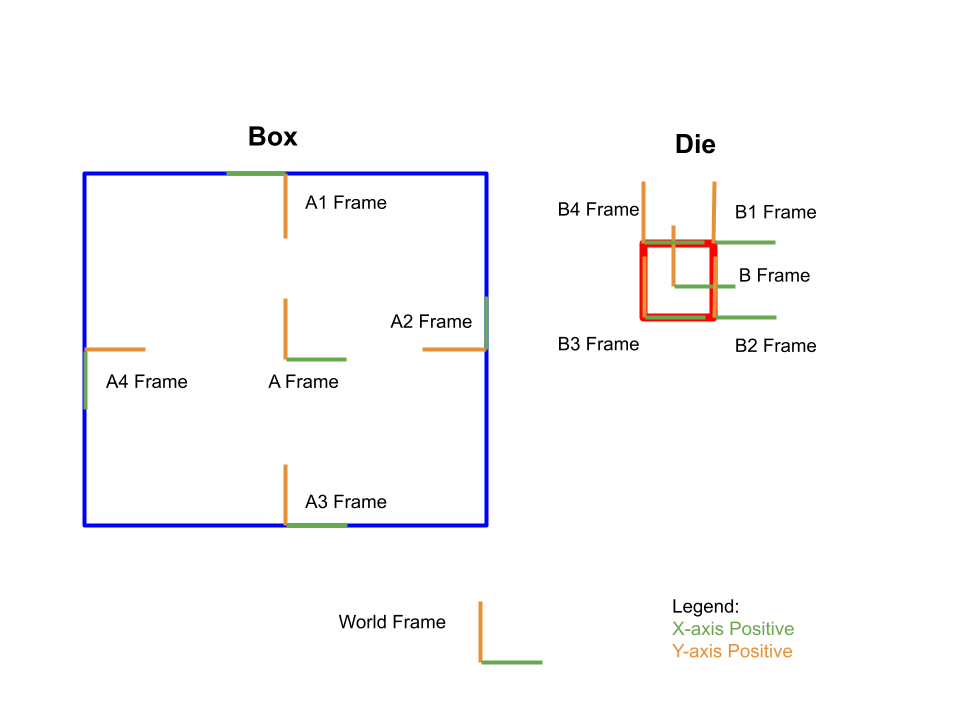
To simulate this system, transformation matrices are used to represent the position and orientation of the two objects in the world frame. From these dynamic transformations, static transformations from the centers are used to model the edges of the box and corners of the die. These are then used for impact, and the frame directionality is used for ease of calculation. These frames can be seen from the image below.
Euler Lagrange Equations
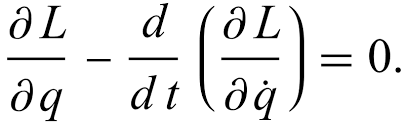
The Euler-Lagrange equations (shown in terms of L(q,qdot) above) are critical for finding the instantaneous accelerations of the bodies. By finding the body velocities of the box and the die, defining the inertial matrices, and calculating the kinetic energy and potential energy (so that we have the Lagrangian, L), the equation shown above can be calculated for each component of the configuration q. From these equations, the accelerations of the configuration are found, and the system is simulated using RK4 integration over a 0.01 second timestep.
Constraints
The system is constrained by the impacts that keep the red die inside the blue box. Whenever an impact is detected by one of the 4 corners of the contacting one of the 4 edges of the box, the impact update equations will trigger in the simulation loop to reflect the appropriate dynamics of the system. Each collision is considered a fully elastic collision between bodies which can be seen from the video above.
External Forces
There are two external forces acting on the system in this simulation. First, is a force that is equal to the force of the box due to gravity to keep it up. This force does not account for the impact of the die on the box, so it does fall slightly due to intertia as they impact each other. The second force is a rotation force on the box to give it an initial rotational velocity. This force has an inverse relationship with time so it provides an initial acceleration that decreases throughout the simulation.
